Angle Relationships Names Unpacked

You know, sometimes, in our daily routines, we might not even notice the simple, yet rather powerful, geometric patterns all around us. Think about it for a second; from the sharp corners of a picture frame to the way a road crosses another, angles are, like, everywhere. And, you know, it's not just about how wide or narrow an angle appears, but also how they interact with each other. These interactions, actually, have their own special labels, which helps us talk about them more clearly.

Getting a handle on these different kinds of angle relationships names can really help you see the world a little differently, in a way. It’s a bit like learning the names of family members; once you know who’s related to whom and how, you can understand the whole family tree much better. These relationships are, you know, fundamental to so many things, from building houses to designing video games. It’s pretty cool, actually, how these basic ideas sort of build up to bigger concepts.

So, we're going to take a closer look at these common ways angles connect with each other. We will, you know, explore what makes each type unique and how they play a part in the shapes and structures we encounter every day. It's really just about giving a name to something you probably already see, but maybe haven't really thought about in this particular way. This will, hopefully, make geometry feel a little less abstract and, well, a bit more relatable, perhaps.

• Fast And Furious 7 Actors
• Jelena Djokovic Nationality
• Christopher French Movies And Tv Shows
• Lana Nelson
• Mirjam Poterbin

Please note: The "My text" provided does not contain information relevant to "angle relationships names." Therefore, this blog post will not reference the provided text but will adhere to all other formatting and stylistic requirements.

Table of Contents

• What are Angle Relationships Names, anyway?
• Opposite Corners - Vertical Angle Relationships Names
• Angles on a Straight Line - Linear Pair Angle Relationships Names
• Making a Right Angle - Complementary Angle Relationships Names
• Adding Up to a Straight Line - Supplementary Angle Relationships Names
• Do Angles Ever Just Sit Next to Each Other? - Adjacent Angle Relationships Names
• Angles with a Transversal - Exploring Special Angle Relationships Names
  • Inside the Lines - Alternate Interior Angle Relationships Names
  • Outside the Lines - Alternate Exterior Angle Relationships Names
  • Matching Spots - Corresponding Angle Relationships Names
  • Same Side Inside - Consecutive Interior Angle Relationships Names
• Why Do We Even Talk About Angle Relationships Names?
• How Can You Spot These Angle Relationships Names in Everyday Stuff?

What are Angle Relationships Names, anyway?

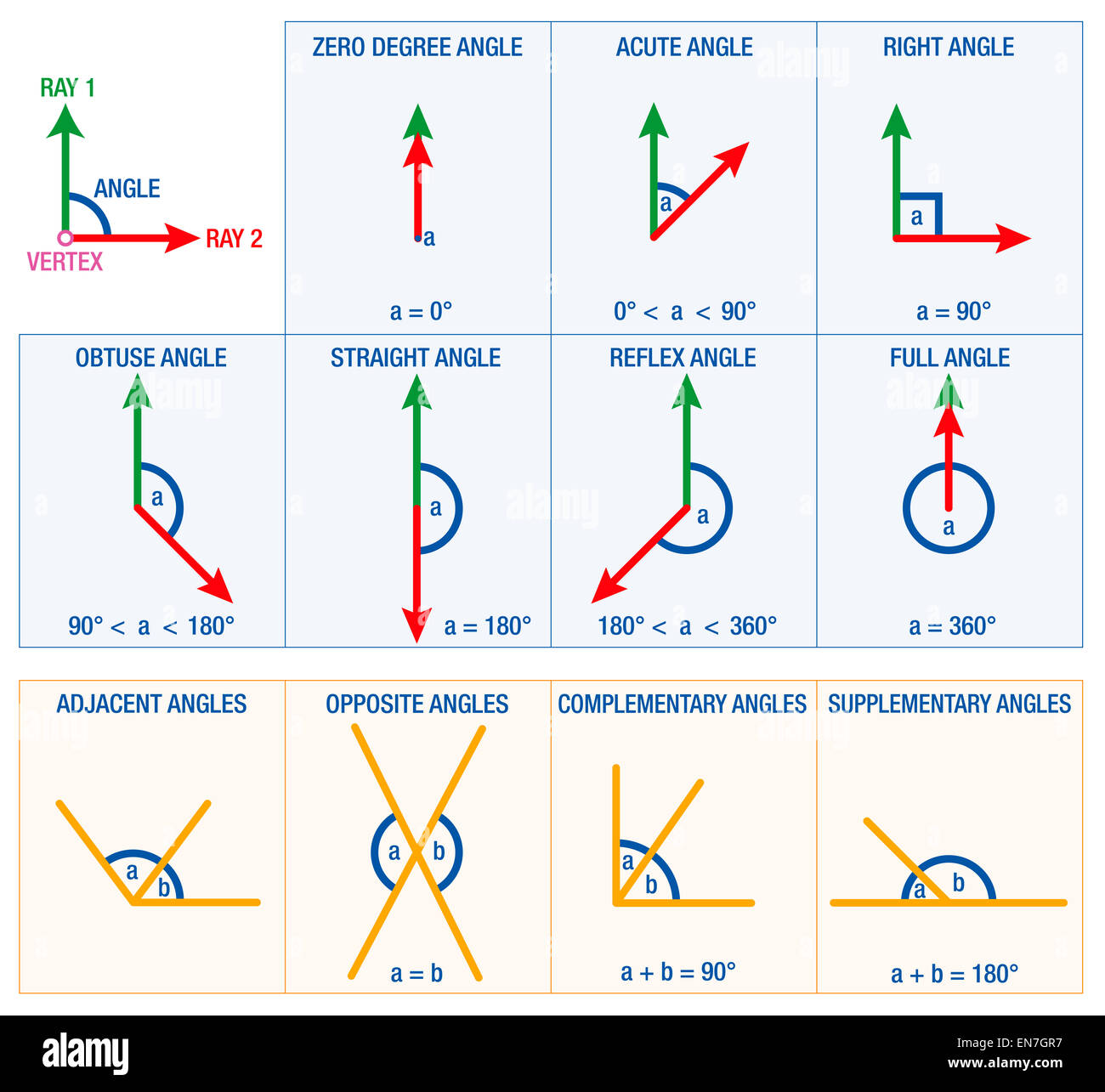
Well, to be honest, when we talk about angle relationships names, we're really just giving labels to how angles hang out together. Imagine, for instance, two angles that share a common side, or perhaps two angles that are formed when lines cross. These connections aren't random; they follow certain rules and, you know, patterns that we can observe and describe. Giving them specific names helps us communicate about them without having to draw a picture every single time, which is pretty handy.

It's like having a shorthand for describing how different parts of a shape fit together. For example, if you hear someone mention "complementary angles," you instantly get a picture of two angles that, when put together, form a perfect corner. This makes discussions about geometry, like, way more efficient. So, these names are, in a way, just tools for clear communication in the world of shapes and lines.

• James Kambewa
• Kal El Cage
• 50 Cent Age
• Tsrmommyduties
• Jake Bongiovi Movies

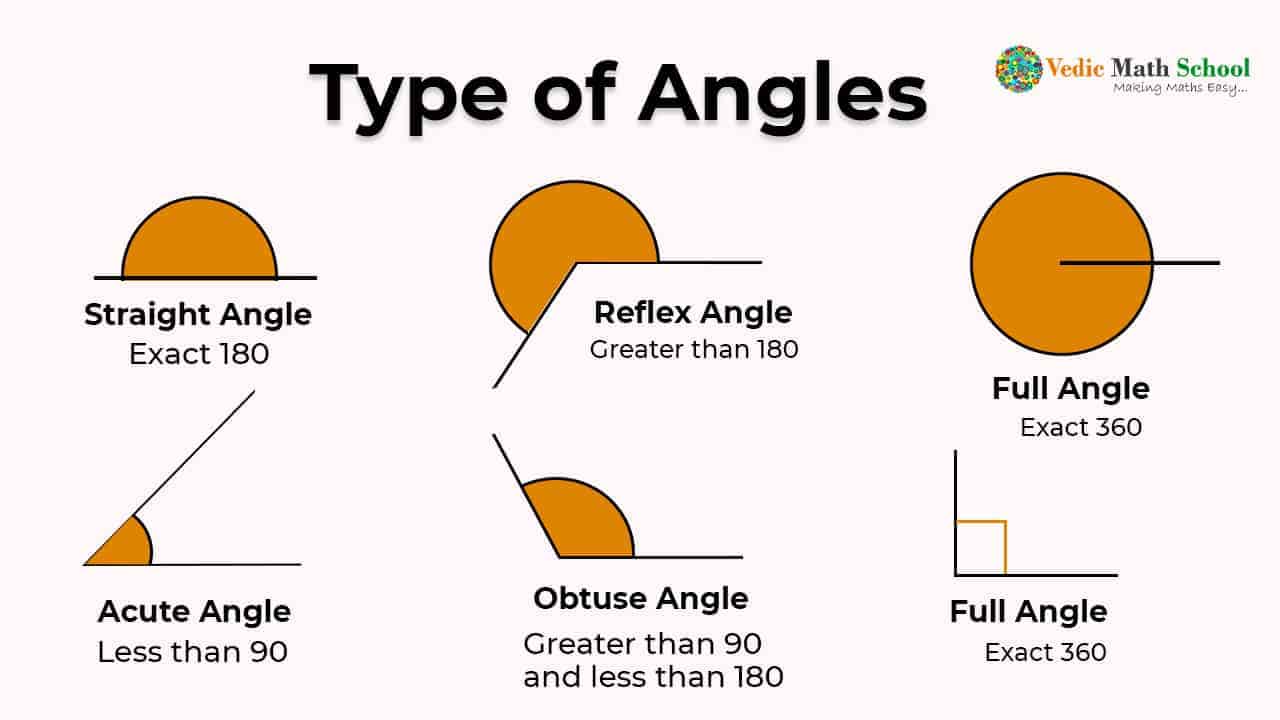
Every single one of these angle relationships names has a particular characteristic that sets it apart. Some are about angles adding up to a specific amount, while others describe their position relative to each other. We will, you know, go through each one, so you can sort of build a mental picture of what they look like and how they work. It's actually a lot less complicated than it might sound at first, I promise.

Opposite Corners - Vertical Angle Relationships Names

So, imagine two straight lines crossing each other, just like a big 'X'. When this happens, you get four angles, right? The angles that are directly across from each other, like the top one and the bottom one, or the left one and the right one, are called vertical angles. And, you know, here's the cool part: these opposite angles are always, always the same size. It's a pretty consistent rule, actually.

Think about a pair of scissors opening and closing. As you open them, the angle at the pivot point and the angle formed by the handles on the opposite side will always be identical. That's a real-world example of vertical angle relationships names in action. It's a simple idea, yet it pops up in so many places, from bridge designs to the way light bounces off surfaces, in a way.

This property, that vertical angles are equal, is super useful in geometry. If you know the size of one angle, you immediately know the size of its vertical partner without having to measure anything else. It saves a lot of time and effort, and, you know, it's one of those foundational bits of knowledge that helps you solve bigger problems down the line. It's pretty neat, honestly, how consistent these things are.

Angles on a Straight Line - Linear Pair Angle Relationships Names

Now, let's think about a straight line. If you have a point on that line, and another line or ray starts from that point and goes off in some direction, it divides the straight line into two angles. These two angles, sitting side-by-side on a straight line, form what we call a linear pair. And, you know, the defining characteristic of these angle relationships names is that they always add up to 180 degrees, which is the measure of a straight line.

Picture a door opening. The angle formed by the door and the wall, plus the angle formed by the door and the space it's opening into, combine to make a straight line if the door opens fully flat against the wall. That's, like, a linear pair right there. Or consider a clock face; if the hands form a straight line, any two adjacent angles that make up that straight line would be a linear pair. It's a fairly common sight, you know.

Knowing that a linear pair always sums to 180 degrees is, actually, incredibly helpful for finding missing angle measurements. If you know one angle in a linear pair, you can easily figure out the other by simply subtracting from 180. It's a very straightforward calculation, and, you know, it’s another one of those basic angle relationships names that gets used a lot in practical applications, from construction to even, like, sports.

Making a Right Angle - Complementary Angle Relationships Names

Okay, so what if two angles, when you put them together, make a perfect corner, like the corner of a book or a table? Those two angles are called complementary angles. Their sum, you know, always adds up to exactly 90 degrees. This is, like, super important because right angles are everywhere in our built environment, from walls meeting floors to the way most picture frames are put together.

Imagine, for instance, a slice of pizza cut into two pieces, where the two cuts form a right angle at the center. Each of those slices, if they add up to that perfect corner, would be complementary to the other. Or think about a ladder leaning against a wall; the angle the ladder makes with the ground and the angle it makes with the wall, assuming the wall is perfectly vertical and the ground is flat, could be complementary in certain scenarios, more or less.

The concept of complementary angle relationships names is pretty vital in fields like carpentry, architecture, and even in art. Knowing that two angles combine to form a right angle allows for precise measurements and constructions. It means you can, like, ensure things are square and true, which is, you know, really important for stability and appearance. It's a basic but powerful idea, honestly.

Adding Up to a Straight Line - Supplementary Angle Relationships Names

Similar to linear pairs, but not always adjacent, supplementary angles are any two angles that, when you add their measurements together, give you a total of 180 degrees. While a linear pair is a specific type of supplementary angle where the angles are right next to each other on a straight line, supplementary angles don't necessarily have to be side-by-side. They just need to sum to that 180-degree mark, you know.

Consider, for example, the angles inside a triangle. While not directly supplementary to each other in a pair, the sum of all three angles in a triangle is always 180 degrees. This is a bit different, but it shows the significance of the 180-degree sum. A more direct example for supplementary angle relationships names might be the angle a ramp makes with the ground, and the angle the ground would make with the ramp if it continued upwards – those two would add up to 180 degrees, typically.

This idea is, you know, very useful in many areas. For instance, in navigation, understanding supplementary angles can help in plotting courses or determining directions. If you know one angle, finding its supplement is just a matter of subtracting from 180, which is, like, super simple. It’s a very practical concept that helps with problem-solving in geometry and beyond, honestly.

Do Angles Ever Just Sit Next to Each Other? - Adjacent Angle Relationships Names

Yes, they do! When two angles share a common side and a common vertex (that's the point where the lines meet), and they don't overlap, they are called adjacent angles. Think of them as next-door neighbors in the world of angles. They are, you know, right beside each other, sharing a boundary but having their own distinct spaces. This is a very common arrangement you'll see in all sorts of shapes.

Imagine a slice of pie cut into two smaller pieces from the same larger slice. The two smaller angles formed by those cuts, sharing the center point of the pie and the line where they meet, would be adjacent. They don't have to add up to a specific total, like 90 or 180 degrees; their relationship is purely about their position relative to each other. It's just about being next to one another, basically.

While adjacent angle relationships names don't always have a fixed sum, they are a fundamental building block for understanding other angle relationships. For example, a linear pair is a specific type of adjacent angle relationship. Knowing an angle is adjacent to another can give you clues about how they might interact, especially when other lines or shapes are involved. It's a pretty simple concept, but important, you know.

Angles with a Transversal - Exploring Special Angle Relationships Names

When a line, which we call a transversal, cuts across two or more other lines, it creates a whole bunch of angles. These angles, you know, have some very specific relationships, especially if the lines being cut are parallel. It's like a special family reunion where everyone has a particular connection to someone else. These angle relationships names are super important in things like architecture and engineering, where parallel lines are, like, everywhere.

Inside the Lines - Alternate Interior Angle Relationships Names

So, when a transversal cuts two parallel lines, the angles that are on opposite sides of the transversal and between the two parallel lines are called alternate interior angles. And, you know, if those two main lines are indeed parallel, these angles will always be equal in size. It's a very reliable rule, actually. Think about the 'Z' shape formed by the lines; the angles inside the 'Z' corners are alternate interior angles.

Outside the Lines - Alternate Exterior Angle Relationships Names

Similarly, alternate exterior angles are on opposite sides of the transversal but outside the two parallel lines. Just like their interior counterparts, if the two main lines are parallel, these alternate exterior angle relationships names will also be equal in measurement. Imagine the 'Z' shape again, but this time, the angles are on the outer corners of the 'Z'. It's pretty consistent, you know.

Matching Spots - Corresponding Angle Relationships Names

Corresponding angles are in the same relative position at each intersection where the transversal crosses the parallel lines. For example, the top-left angle at the first intersection and the top-left angle at the second intersection would be corresponding angles. And, you know, if the lines are parallel, these corresponding angle relationships names are always equal. It's like they're sitting in the same seat at two different tables, basically.

Same Side Inside - Consecutive Interior Angle Relationships Names

These are also known as same-side interior angles. They are on the same side of the transversal and between the two parallel lines. Unlike alternate interior angles, these consecutive interior angle relationships names are not equal. Instead, if the lines are parallel, they are supplementary, meaning they add up to 180 degrees. It's a bit different, but still a very predictable relationship, you know.

Why Do We Even Talk About Angle Relationships Names?

You might be thinking, "Why bother with all these specific angle relationships names?" Well, the truth is, they're not just abstract concepts for math class. They are, actually, incredibly practical. Knowing these relationships helps engineers design stable bridges, architects plan buildings that stand tall, and even video game developers create realistic environments. They are, like, the basic language of shapes and structures, in a way.

For instance, if you're building a roof, understanding complementary and supplementary angles helps you cut the wood pieces correctly so they fit together perfectly and support the structure. Or, if you're, you know, laying tiles, knowing about vertical angles helps you ensure your patterns line up neatly. It's all about precision and predictability, which is pretty important for making things work.

These angle relationships names also form the foundation for more advanced mathematical concepts. They help us, you know, prove theorems, solve complex geometric problems, and even understand physics, like how light reflects or refracts. So, while they might seem simple, they are, actually, very powerful tools for understanding the physical world around us, basically.

How Can You Spot These Angle Relationships Names in Everyday Stuff?

It's actually pretty fun to start noticing these angle relationships names once you know what to look for. Take a moment, for example, to observe the corners of a room. The walls meet the floor at right angles, which means the angles formed are complementary if you consider the internal and external parts of the corner. Or, you know, look at a pair of scissors; as mentioned before, the angles formed by the blades and handles demonstrate vertical angles.

Think about a railroad track with another track crossing it. That's a perfect real-world example of a transversal cutting parallel lines, and you can, like, spot all sorts of alternate interior, alternate exterior, and corresponding angle relationships names there. The way the lines intersect creates these predictable patterns, which is, you know, quite fascinating once you start paying attention.

Even something as simple as opening a book can show you adjacent angles. The angle of one page relative to the spine, and the angle of the next page, are adjacent. The more you, you know, look around with these angle relationships names in mind, the more you'll realize just how fundamental they are to the design and stability of pretty much everything man-made, and even many natural formations. It's a bit like learning a new language and suddenly being able to read the world around you, basically.

So, we've explored several key angle relationships names: vertical angles, linear pairs, complementary angles, supplementary angles, and adjacent angles. We also looked at the special relationships that pop up when a transversal line cuts across others, like alternate interior, alternate exterior, corresponding, and consecutive interior angles. Getting a handle on these ideas, you know, really helps us talk about and understand the shapes and structures all around us.